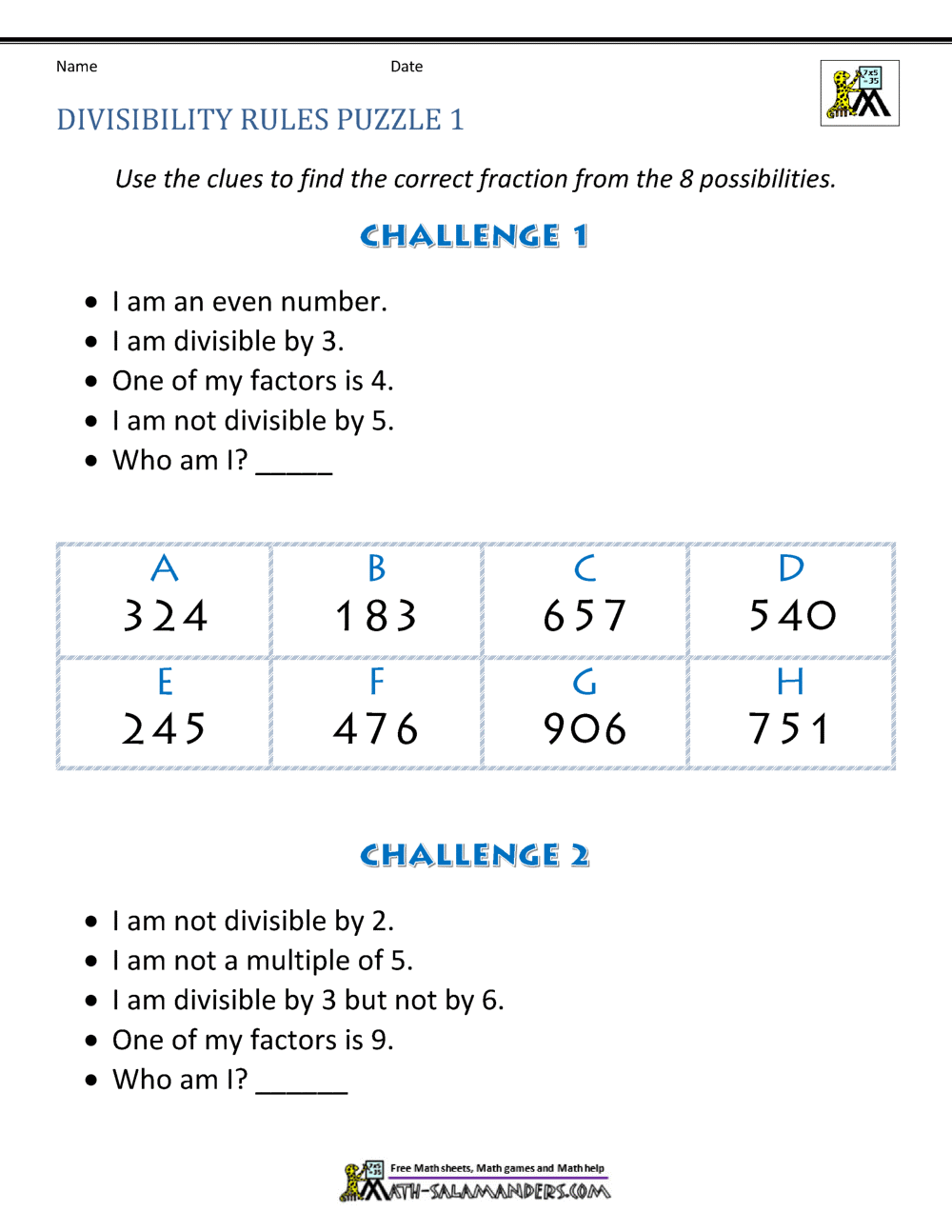
Divisibility Rules Printable Worksheet: A Comprehensive Guide to Number Theory
In the realm of mathematics, divisibility rules serve as a powerful tool for simplifying complex calculations and understanding the intricate relationships between numbers. This comprehensive divisibility rules printable worksheet delves into the fascinating world of number theory, providing a clear and concise overview of divisibility criteria for various numbers.
From the fundamental rules of divisibility by 2 to the more advanced techniques for determining divisibility by 12, this worksheet offers a structured approach to mastering these essential concepts. With a focus on practical application and real-world examples, it empowers learners to tackle divisibility problems with confidence and efficiency.
Divisibility Rules Table
Yo, check this out! This table’s got the divs for all the numbers from 2 to 12. It’s like a cheat sheet for when you’re trying to figure out if a number is divisible by another number.
Here’s the deal: a number is divisible by another number if it can be divided by that number without leaving a remainder. For example, 12 is divisible by 3 because 12 ÷ 3 = 4 with no remainder. But 12 is not divisible by 5 because 12 ÷ 5 = 2 with a remainder of 2.
Divisibility Rules Table
| Divisor | Rule | Example |
|---|---|---|
| 2 | Even number (last digit is 0, 2, 4, 6, or 8) | 12, 24, 36 |
| 3 | Sum of digits is divisible by 3 | 12 (1 + 2 = 3), 27 (2 + 7 = 9) |
| 4 | Last two digits are divisible by 4 | 24 (24 is divisible by 4), 36 (36 is not divisible by 4) |
| 5 | Last digit is 0 or 5 | 10, 15, 25 |
| 6 | Divisible by both 2 and 3 | 12 (divisible by 2 and 3), 24 (divisible by 2 and 3) |
| 8 | Last three digits are divisible by 8 | 248 (248 is divisible by 8), 368 (368 is not divisible by 8) |
| 9 | Sum of digits is divisible by 9 | 18 (1 + 8 = 9), 27 (2 + 7 = 9) |
| 10 | Last digit is 0 | 10, 20, 30 |
| 11 | Alternating sum of digits is divisible by 11 | 121 (1 – 2 + 1 = 0), 231 (2 – 3 + 1 = 0) |
| 12 | Divisible by both 3 and 4 | 12 (divisible by 3 and 4), 24 (divisible by 3 and 4) |
Divisibility by 3
Blud, let’s chat about divisibility by 3, fam. It’s dead easy, so listen up.
The rule is: if the sum of all the digits in a number is divisible by 3, then the number itself is divisible by 3. Capiche?
Examples
- Take 123, for example. 1 + 2 + 3 = 6, which is divisible by 3. So, 123 is also divisible by 3.
- Another one: 456. 4 + 5 + 6 = 15, which is divisible by 3. Bingo, 456 is divisible by 3 as well.
Non-Examples
- Now, let’s flip it. 124. 1 + 2 + 4 = 7, which isn’t divisible by 3. So, 124 ain’t divisible by 3 either.
- Same deal with 578. 5 + 7 + 8 = 20, not divisible by 3. Hence, 578 is a no-go for divisibility by 3.
Divisibility by 4
Innit, the rule for divisibility by 4 is a doddle. If the last two digits of a number are divisible by 4, then the whole number is divisible by 4.
For example, 124 is divisible by 4 because the last two digits, 24, are divisible by 4. However, 125 is not divisible by 4 because the last two digits, 25, are not divisible by 4.
Relationship between Divisibility by 4 and the Last Two Digits
This rule is based on the fact that 4 is a multiple of 2 and 2, so if the last two digits of a number are divisible by 2, then the whole number is divisible by 4.
Divisibility by 6
Divisibility by 6 is a bit like being the best friend of both 2 and 3. If a number is divisible by both 2 and 3, then it’s automatically divisible by 6.
Divisibility Rule for 6
The divisibility rule for 6 is simple: a number is divisible by 6 if it’s divisible by both 2 and 3.
Examples
Let’s see some examples:
– 12 is divisible by 6 because it’s divisible by both 2 (12 ÷ 2 = 6) and 3 (12 ÷ 3 = 4).
– 18 is also divisible by 6 because it’s divisible by both 2 (18 ÷ 2 = 9) and 3 (18 ÷ 3 = 6).
Non-Examples
Here are some non-examples:
– 5 is not divisible by 6 because it’s not divisible by 2 (5 ÷ 2 = 2 remainder 1).
– 10 is divisible by 2 (10 ÷ 2 = 5) but not by 3 (10 ÷ 3 = 3 remainder 1), so it’s not divisible by 6.
Relationship to Divisibility by 2 and 3
So, if you want to check if a number is divisible by 6, just check if it’s divisible by both 2 and 3. It’s like a shortcut that saves you time!
Divisibility by 8
Yo, listen up! We’re gonna drop some knowledge on how to tell if a number’s divisible by 8. It’s a piece of cake, innit?
First off, check out the last three digits of the number. If they’re divisible by 8, then the whole number is too. It’s like a magic trick, blud!
For example, let’s take 248. The last three digits, 48, are divisible by 8, so the whole number is as well.
But hold your horses! Not all numbers that end in 8 are divisible by 8. Take 18, for instance. The last three digits are 018, which ain’t divisible by 8. So, the whole number isn’t either.
Now, here’s a tip that’ll blow your mind: if the last three digits of a number are divisible by 4, then the number is also divisible by 8. It’s like a shortcut, bruv!
So, next time you’re trying to figure out if a number’s divisible by 8, just check out the last three digits. It’s a foolproof way to know for sure. Peace out!
Divisibility by 9
Divisibility by 9 is a handy rule that can help you quickly determine if a number is divisible by 9 without having to perform long division. The rule states that a number is divisible by 9 if the sum of its digits is divisible by 9.
For example, the number 123 is divisible by 9 because the sum of its digits (1 + 2 + 3 = 6) is divisible by 9. Similarly, the number 456 is divisible by 9 because the sum of its digits (4 + 5 + 6 = 15) is divisible by 9.
On the other hand, the number 124 is not divisible by 9 because the sum of its digits (1 + 2 + 4 = 7) is not divisible by 9. Likewise, the number 457 is not divisible by 9 because the sum of its digits (4 + 5 + 7 = 16) is not divisible by 9.
The divisibility rule for 9 is a useful tool that can save you time and effort when working with numbers. It is especially helpful when you need to quickly determine if a number is divisible by 9 without having to perform long division.
Divisibility by 10
The divisibility rule for 10 is straightforward: a number is divisible by 10 if and only if its last digit is 0. This rule applies to all whole numbers, positive or negative.
Examples and Non-examples
- Examples: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 1000, 10000
- Non-examples: 11, 12, 13, 14, 15, 16, 17, 18, 19, 101, 102, 103
Relationship with Last Digit
The divisibility rule for 10 is closely related to the value of the last digit. The last digit of a number represents the remainder when the number is divided by 10. For example, the last digit of 123 is 3, which means that 123 divided by 10 leaves a remainder of 3.
Therefore, a number is divisible by 10 if and only if its last digit is 0. This is because a number with a last digit of 0 is divisible by 10 without leaving a remainder.
Divisibility by 11
Divisibility by 11 is determined by an alternating addition and subtraction method, where digits are alternately added and subtracted from right to left.
Alternating Addition and Subtraction Method
1. Start from the rightmost digit.
2. Add the digit to the next digit on the left.
3. Subtract the result from the next digit on the left.
4. Continue alternating addition and subtraction until you reach the leftmost digit.
5. If the final result is 0 or 11, the number is divisible by 11. Otherwise, it is not.
Divisibility by 12

A number is divisible by 12 if it is divisible by both 3 and 4.
Relationship to Divisibility by 3 and 4
Since 12 is the product of 3 and 4, a number is divisible by 12 if it is divisible by both 3 and 4.
- If a number is divisible by 3, its sum of digits is divisible by 3.
- If a number is divisible by 4, its last two digits form a number divisible by 4.
FAQs
What is the divisibility rule for 3?
A number is divisible by 3 if the sum of its digits is divisible by 3.
How do I check if a number is divisible by 4?
A number is divisible by 4 if the last two digits are divisible by 4.
What is the relationship between divisibility by 6 and divisibility by 2 and 3?
A number is divisible by 6 if it is divisible by both 2 and 3.
How do I determine if a number is divisible by 11?
To check divisibility by 11, alternate adding and subtracting the digits, starting from the rightmost digit. If the result is 0 or a multiple of 11, the number is divisible by 11.